The Murderous Maths Sieve of Eratosthenes

In The Murderous Maths of Everything we meet several ancient Greek mathematicians including ERATOSTHENES. Eratosthenes did lots of rather neat things, but he's best known for his method of finding prime numbers. This is called the Sieve of Eratosthenes.

This is our version of the sieve as it appears in the book, but here we're going to show you a couple of extra details that the book didn't have space for.

We're going to find all the prime numbers up to 100. We start by writing them out in a square grid, and then we work along the numbers and “sieve” out all the numbers that are not prime.

• The first number is 1 but we’ll ignore it because when it comes to prime numbers, 1 is a naughty little number who just causes arguments.
• Move on to the next number after 1 which is 2. We put a nice little green box around it. We then go through and colour in every second number that comes after it. (i.e. all the numbers that divide by 2.)
• The next number after 2 is 3, and as it hasn’t been coloured in, that means it’s also a prime number. We put a blue box around the 3 and colour in every third number after it that isn't already coloured. (You’ll find the lowest number we colour is 3 × 3 = 9)
• After 3 the next number is 4 but that’s already been coloured in which means it isn't prime. So we move on to 5, we put an orange box round it and colour every 5th number after it. (The lowest number we colour is 5 × 5 = 25)
• The next unmarked number is 7 so we box it in purple and colour in every 7th number. (Yes, 7× 7 = 49 is the lowest!)
• We have now finished the top row of the square. This means that all the numbers up to 100 that are NOT primes are coloured in, and all the prime numbers are either boxed or left blank.

Why don't we need to work beyond the top row of the square? If we move on to the next unmarked number, we find it's 11. If we boxed it and then tried to colour the first unmarked number that divides by 11, that would be 11 x 11 = 121. This is bigger than 100 so we don't need it! That's why we started out by putting our numbers in a square. Once we've finished working along the top row, we can be confident that it's time to stop!

Why did we ignore the number 1? In the book you'll see how the EVIL NUMBER 1 causes all sorts of problems, especially with prime numbers. If we boxed the number 1 then coloured in every number that divides by 1, we'd end up colouring in ALL the numbers! That wouldn't get us very far so that's why we ignored it.

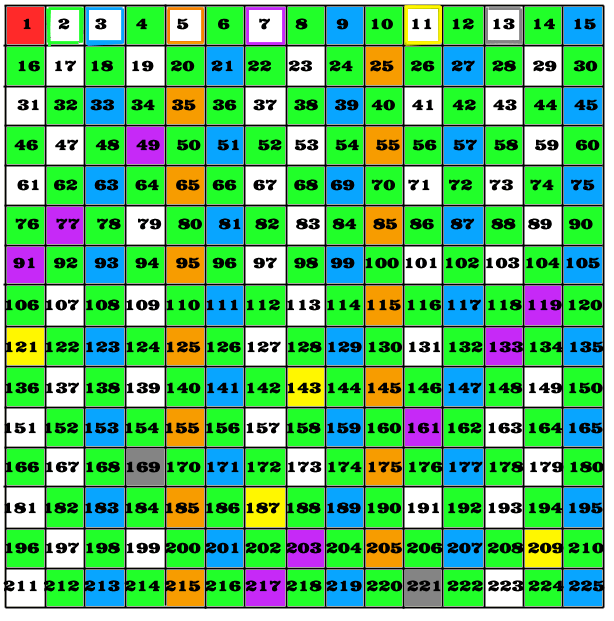If you wanted to find all the primes up to 200, you need to make a square measuring 15 x 15. (This will actually give you all the primes up to 225.) You just work along the top row in the same way, and when you've finished all the primes will be revealed!

If you like numbers (and some people do!) it's interesting to see the odd little patterns that emerge when you make these grids. Here you'll notice how the green "2" boxes form a chequerboard pattern and how the purple "7" boxes are all in diagonals...

...but the thing that has been bothering mathematicians for thousands of years is that it doesn't matter how the number grid is laid out, they can't make the white prime boxes fall into ANY kind of pattern!

The Murderous Maths of Everything

The Prime Number Calculator

The Prime Counter

Murderous Maths Home Page