
What are the chances of 366 strangers all having a different birthday?
The question sounds EASY enough, but as you'll see, the answer is EVIL.
This is one of the fiddliest sums we've ever had to think about, so let's approach it slowly. Good luck!
What are the chances of 2 strangers in a room having a different birthday?
To keep it simple, we'll start by saying there are 365 days in every year.
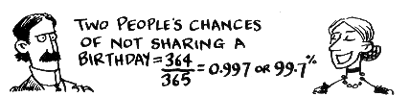
- The first person can have their birthday on any day of the year.
- When the second person turns up, their chance of having the same birthday is 1/365.
- So the chance of two people having a different birthday is 364/365.
What are the chances of 3 strangers in a room having a different birthday?
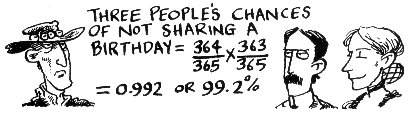
- When the third person comes into the room, so long as the first two have different birthdays, then the third person's chance of also being different is 363/365.
- To find the chance of all three people having different birthdays we multiply these two chances together. We get 364/365 x 363/365 which we can write as (364 x 363)/3652.
What are the chances of 23 strangers in a room having a different birthday?
 There's a reason for jumping ahead to 23!
There's a reason for jumping ahead to 23!
- When the fourth person comes into the room we multiply by 362/365 then for the fifth person we multiply by 361/365.
- By the time the 23rd person has come in the final sum is (364 x 363 x 362 x ... all the way down to ... x 344 x 343) / 36522.
- When you work this out you find the chance of them all having a different birthday is 49.27%.
- Therefore the chance of at least two people sharing a birthday is 50.73% which means that in a room of 23 strangers it's slightly more likely that two people WILL share a birthday!
All this stuff is quite well known, and there's a whole chapter on it in Do You Feel Lucky?. In fact if you have 30 strangers in a room there's about a 70% chance that at least two will share a birthday.
But so far all the calculations have assumed there are exactly 365 days in every year.
Unfortunately for us, when the book Easy Questions Evil Answers was being put together, we were asked:
What are the chances that 366 strangers in a room will all have a different birthday?
|
What we're saying here is that for every different date in the year, one person must have that birthday, and that includes one person who has a birthday on February 29th!
It's February 29th that gives the problems. Most years have 365 days in them and February only has 28 days. But every fourth year is a leap year and there is an extra day in February making a total of 366 days. Therefore we need to base our sums on the total number of days in four years which is: 3 x 365 + 366 = 1461.
- Let's suppose that the first person to come into our room happens to be the person who's birthday is Feb 29th. The chances of that are 1/1461.
- When the second person comes in, the only date they can't have a birthday on is Feb 29th, so the chance of the second person being different is 1460/1461.
- Now let's say, for example, the second person's birthday was on October 5th. Out of a four-year period of 1461 days there are four October 5ths. Therefore when the third person comes into the room there are a total of FIVE days they can't have a birthday on. (That's four Oct 5ths and one Feb 29th.) So the third person's chance of being different is 1456/1461. The chances of all three being different are:
1/1461 x 1460/1461 x 1456/1461
- When the fourth person comes in, their chance of a different birthday is 1452/1461, and for the fifth person it's 1448/1461.
- By the time the 366th person has come into the room, if everybody else has had a different birthday then there will only be one calendar date left e.g. July 24th. In a period of 1461 days, there are only four of these, so the 366th person's chances of being different from everybody else are 4/1461.
- Multiply the whole lot together! You get:
1/1461 x 1460/1461 x 1456/1461 x ... all the way to ... x 8/1461 x 4/1461
- There are 366 fractions here all with 1461 on the bottom, so this all simplifies to:
(1 x 1460 x 1456 x 1452 x ... 8 x 4)/1461366. But of course we don't need to put in the 1x at the front, so it becomes:
(1460 x 1456 x 1452 x ... 8 x 4)/1461366
- There are 365 numbers in the bracket and they will each break down like this: 1460 = 365 x 4 and 1456 = 364 x 4 and 1452 = 363 x 4 and so on. So if we divide every term in the bracket by 4 and bring all the 4's outside we get:
4365 x (365 x 364 x 363 x ... all the way to ... x 3 x 2 x 1)/1461366
The bit in the bracket is a factorial which we can write like this: 365!
- So putting the whole lot together the chances of the first person in the room having a birthday on Feb 29th, and then the other 365 people all being different are:
(4365 x 365! ) / 1461366
- Finally... we have to allow for the fact that our Feb 29th birthday person could come into the room at any time, rather than having to be first. Supposing everyone was lined up to get into the room. How many different positions in the line could he stand in? The answer is 366. So we multiply our last answer by 366 and at last we get the answer we're looking for:
(366 x 4365 x 365! ) / 1461366
- We can make this a tiny bit neater, because 366 x 365! = 366! So at last, here is the sum to work out the chances of 366 strangers in a room all with different birthdays:
- This works out to be about 1 chance in 3520000000000000000000000000000000000000000000000000000000000000000000000000000
0000000000000000000000000000000000000000000000000000000000000000000000000000000.
(There are 155 zeros there.)

|

You can even win bets with birthdays! You'll find all the details in here, along with lots of other calendar chaos including why Friday 13th is more likely than any other day of the week, and which country had a freak February 30th.
There are also green moons, paradoxes, tricks and numbers so big that they wouldn't fit in the universe.
Click on the cover for details!

|
 So did you understand all that? We have to thank our resident expert Michael Jones for working this out for us. And just in case you can't quite comprehend how unlikely 366 strangers having different birthdays is, Michael explains it like this:
So did you understand all that? We have to thank our resident expert Michael Jones for working this out for us. And just in case you can't quite comprehend how unlikely 366 strangers having different birthdays is, Michael explains it like this:
Suppose every atom in the universe had a birthday and you divided them all into groups of 366, you'd need as many separate universes as there are atoms in this one before it became at all likely that somewhere in one of the universes there was a group of 366 atoms with different birthdays!
And by the way... Michael was a bit worried that his answer isn't ABSOLUTELY accurate because it doesn't allow for the fact that we didn't have a Feb 29th in 1900 and there won't be one in 2100 or 2200 or 2300. If we were going to worry about that, then we'd need to use 366 fractions that had the number 146,097 on the bottom and that would be too evil even for us! We're not mad, you know.

Do You Feel Lucky?
Easy Questions Evil Answers
Murderous Maths Home Page
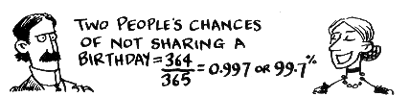

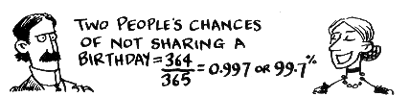
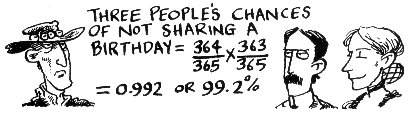
 There's a reason for jumping ahead to 23!
There's a reason for jumping ahead to 23!
 So did you understand all that? We have to thank our resident expert Michael Jones for working this out for us. And just in case you can't quite comprehend how unlikely 366 strangers having different birthdays is, Michael explains it like this:
So did you understand all that? We have to thank our resident expert Michael Jones for working this out for us. And just in case you can't quite comprehend how unlikely 366 strangers having different birthdays is, Michael explains it like this:
