The Murderous Maths Research Lab proudly presents...

THE TRAPEZIUM AREA PAGE

This is possibly the most exciting page on the whole internet. Or the dullest. It depends on you.

Trapeziums...

If you have a parallelogram (where both pairs of opposite sides are parallel) or an irregular quadrilateral, then you can't work out the area by just knowing the lengths of the sides! But so long as you know which two sides are parallel, you can work out the area of a trapezium.

The U.S. TRAPEZOID

The US defines a trapezium as having NO parallel sides, and a quadrilateral with just 2 parallel sides is called a TRAPEZOID.
Let's all sing together now:
"You say trapezoid, and we say trapezium...
let's call the whole thing off."
A trapezium is a shape with four sides, two of which are parallel. The sides can all be different lengths. (Note: in the US this shape is called a TRAPEZOID)

Here's one that we photographed earlier.

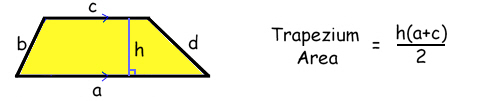
Usually if you want to find the area of a trapezium you use the simple little formula.

In the formula, a and c are the lengths of the two parallel sides, and "h" is the height of the trapezium.
These are the only three measurements you need to work out the area, so before we start getting clever, let's put in some numbers and see what the sums look like.

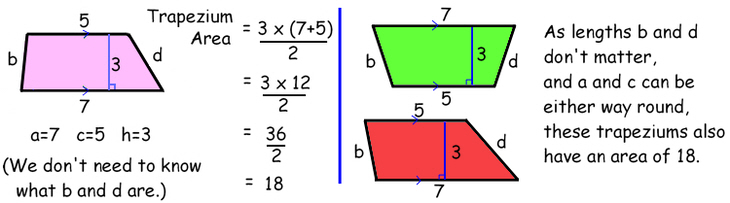
This is probably all you ever need to know about the area of trapeziums, so if you want to leave now, that's fine.

Goodbye!

You now continue at your own risk.

So far it's all been simple BUT...

...we were asked if we could work out the area if we knew the lengths of the four sides, but we DIDN'T know the height! Obviously the usual formula wasn't going to help much, so with the help of some of our regular visitors to this site, we came up with another formula.

The first sensible suggestion came from our Singapore friend Hu Yi Jie. He suggested splitting up the trapezium up into three bits and then attacking the problem like this:

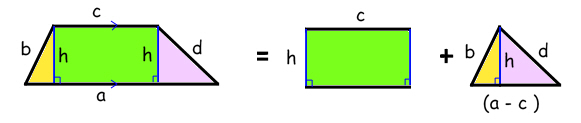
  • You chop off the two triangles at the end to leave a rectangle in the middle. You then put the two triangles together to make one big triangle. We know the lengths of all three sides of this triangle.
    The bottom of the triangle measures (a-c) because the bottom of the trapezium was a, and we have just removed a section that measures c. The other two sides measure b and d.
  • If you've read The Perfect Sausage you'll know about semi-perimeter cows!
    You can work out the area of the triangle using the "semiperimeter" formula.
    This brilliant formula lets you work out the area of a triangle if you know the lengths of the three sides! The "semiperimeter" is half the distance around the triangle so if the lengths of the triangle sides are X,Y and Z then s=½(X+Y+Z). Once we have "s", we get the triangle area with the formula:
            TRIANGLE AREA= (s(s-X)(s-Y)(s-Z))½
    We know that for OUR triangle the side lengths are b,d and (a-c) so first you work out the semiperimeter s=½(b+d+a-c) and then plonk everything into the area formula to get:
    TRIANGLE AREA = (s(s-b)(s-d)(s-(a-c)))½. Nice and easy isn't it?
  • The most common formula for the area of a triangle is AREA = base x height/2. As we now know the area and we already know the base=(a-c) we can work out the height "h" of the triangle.
    So h = 2(s(s-b)(s-d)(s-a+c))½/(a-c)
  • And here's the good bit... the height of the triangle is also the height of the rectangle, so you can then work out the area of the rectangle.
    The rectangle area is c x h therefore the RECTANGLE AREA = 2c(s(s-b)(s-d)(s-a+c))½/(a-c)
  • Add together the areas of the triangle and rectangle... and that's it!

AREA OF TRAPEZIUM = (1 + 2c/(a-c)){s(s-b)(s-d)(s-a+c)}½

where s=½(b+d+a-c)

And when you swap every "s" in the main formula with ½(b+d+a-c) and boil it down you get our formula for the area of a trapezium...

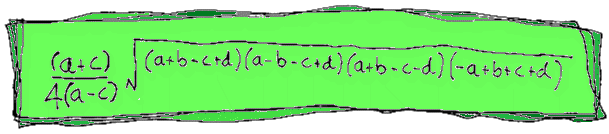
Of course, we've only shown you Hu Yi Jie's EASY version here. We had already worked out another way of solving the problem which we think is even easier. But then we would wouldn't we?

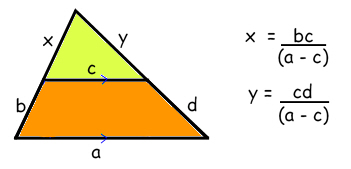
  • First we extended the two non-parallel sides of the trapezium so that they touched. This made two similar triangles.
  • There's enough information to work out the lengths x and y in terms of a,b,c and d.
  • Using the semiperimeter formula again, we worked out the areas of the two triangles and then took the small one away from the big one to leave the area of the trapezium.
Amazingly enough we found that Hu Yi Jie's method produced exactly the same formula as ours did... AND IT WORKS!

We tested it on a trapezium with sides a=30, b=10, c=9 and d=17. This conveniently makes a trapezium of height 8, and it breaks down into a rectangle measuring 9x8 (area=72), and two right angled triangles of 6-8-10 (area=24) and 8-15-17 (area=60). The trapezium area is 72+24+60=156 which is what the formula gives. Oooooh.... we're so pleased with ourselves.

The PYTHAGORAS FORMULA

Many thanks to Timothy Ti'en Ern Ang - yet another young genius from Singapore!
Tim sent us a new trapezium area formula which uses Pythagoras.

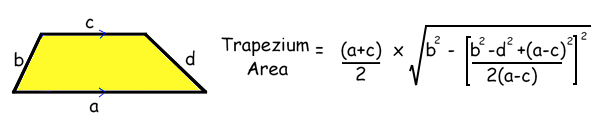
If you compare it to the original simple trapezium formula, you'll see he's found a way to work out the height h using the four sides.


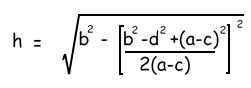
Here's how he did it!

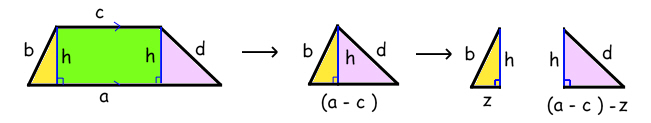
Just in case you're wondering, this web page had been online for 12 years before Tim sent us this. The amazing thing is that Tim is ten years old, so the rest of this page has been on the planet two years longer than Tim has!
And thanks to Kevin Wai who noticed we'd made a mistake when we first put this online! Kevin was seven years old.

If any babies find mistakes, do please get in touch.

You'll find out how algebra
and equations and all this
stuff works in
THE PHANTOM X.
He took the two right-angled triangles off the end and put them together. We know the base of this triangle is (a-c). He then split them up. If the base of one triangle is length z then the base of the other is (a-c)-z = (a-c-z).

For the first triangle, Pythagoras says: b2 = h2 + z2

For the second triangle: d2 = h2 + (a-c-z)2

We'd like to know what z is, so as we have two simultaneous equations, we can subtract the second equation from the first equation to get rid of h. (Some people enjoy this sort of thing.)

b2 - d2 = z2 - (a-c-z)2

Woo-hoo! If we multiply the ugly thing at the end out we get (a-c-z)2 = (a2 - ac -az -ca +c2 + cz - za +zc + z2)
which simplifies to (a2 +c2 +z2 - 2ac -2az + 2cz )

We now put this in place of the (a-c-z)2, not forgetting that there was a minus sign in front of the bracket...

b2 - d2 = z2 - a2 -c2 -z2 + 2ac +2az - 2cz

Hey! There's a +z2 and a -z2 so they disappear...

b2 - d2 = - a2 -c2 + 2ac +2az - 2cz

We now get everything without a z to the same side.

b2 - d2 + a2 -2ac + c2 = 2az - 2cz

And now we conveniently notice that a2 -2ac + c2 factorises to (a-c)2, and the other side factorises too.

b2 - d2 + (a-c)2 = 2z(a-c)

Divide through by 2(a-c), swap the sides over and we've got a value for z. BINGO!

z = [b2 - d2 + (a-c)2 ]/2(a-c)

At this point it's helpful to work out what z2 will be:

z2 = [b2 - d2 + (a-c)2 ]2/[2(a-c)]2

All we do now is go back to our first Pythagoras triangle equation and twiddle it round so we get h2 = b2 -z2 and then put in the z2 value we just worked out.

h2 = b2 - [b2 - d2 + (a-c)2 ]2/[2(a-c)]2

Take a square root of both sides and we get...

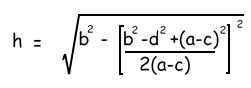
Awesome.

TOUGHER FORMULAS!

A special big cheer to Jenny Wood, and also Carl "Maths Whizz" Turner who both came up with answers using the cosine and sin rules to work out the angles of the trapezium, and then the height and then the area. We haven't tested these formulas, and at the moment we haven't time to explain the COS and SIN rules here. However, if you're a super brainy person we've typed them out as neatly as we can just for YOU and here they are ....

JENNY'S AREA OF TRAPEZIUM = ½(a+c)*b*sin{cos-1[(d2-(a-c)2-b2)/(-2(a-c)b)]}

CARL'S AREA OF TRAPEZIUM = (a+c)(½bd(sin(cos-1(b2+d2-(a-c)2))))/4(a-c)


To the Research Lab

To the Area Calculator Page

To The Perfect Sausage and other Fundamental Formulas

Murderous Maths Main Index Page