

The Sam Loyd Sliding Block Puzzle
|

| ||||||||||||||||||||||||||||||||||||||
|
Sam Loyd's original version was made with 15 wooden blocks in a tray. He offered a reward of $1000 dollars to anyone who could prove they'd done it. Back in the 1870's this was a fortune! All sorts of people claimed they had solved the puzzle, but when they were asked to demonstrate how they'd done it (without actually picking the blocks off the tray and replacing them), none of them could do it. Apparently one clergyman spent a whole freezing winter night standing under a lampost trying to remember what he'd done to get it right. |

|
This clever little programme came from |
TRY IT YOURSELF!We have a little version of the puzzle here.Click on the "New Game" button. The numbers will shuffle up.
|

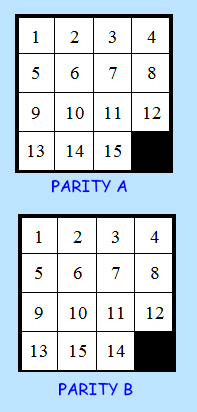
THE MATHS!Let's start with a frightening fact: if you slide the tiles at the rate of one every second to produce a new pattern each time, it will take you over 300,000 years to produce half the possible patterns. And if you think that’s frustrating, what makes it worse is that you won’t be able to create the other half at all! Here’s how the numbers work. If you had the old fashioned wooden blocks, you could take them out and replace them one at a time. You would have 16 choices of what to put in the first position (it could be any one of the 15 blocks or the space.) For the second position you have 15 choices, for the third position you have 14 choices and so on. Therefore the total number of patterns is 16 × 15 × 14 × and so on until ... × 3 × 2 × 1. This kind of sum is called a factorial which we can write as 16! and it multiplies out to give 20,922,789,888,000 different patterns. That’s over twenty billion. However if you don’t take the blocks out and instead you just slide them around, you’ll find that you can only make half of these patterns. That’s because the humble sliding block puzzle has a parity of two. In other words, there are two complete sets of different patterns you can make. Either the blocks will be set up to make one set, or the other set. No pattern appears in both sets. One parity includes the pattern with all the blocks in order, the other parity includes the pattern where the last two blocks are the wrong way round. |
|
 Let's suppose you've got a set of the old puzzle blocks which have been put into the frame at random.
Let's suppose you've got a set of the old puzzle blocks which have been put into the frame at random.
How do you know if you will be able to put them all in the right order?
You need to check two things.
1/ Look at the positions of the numbers and work out how many switches are needed to solve the puzzle. (You’ll see how to do this in a minute.) Most importantly, you need to know if the number of switches is even or odd.
2/  Where is the empty space?
Where is the empty space?
Imagine all the positions on the frame as a chequered grid. If the empty space is on a black square, then the number of switches to solve the puzzle must be EVEN. If the empty space is on a grey square then the number of switches must be ODD.
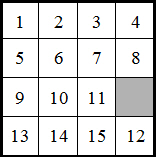 Here we’ve just moved the <12> block one place. In effect it has switched positions with the empty space, so this counts as one switch. The empty space is now in a grey position which means that the number of switches to solve the puzzle must be odd. Of course, to get back to the solved position, we just need one switch to get it back, and as one is an odd number, this puzzle can be solved.
Here we’ve just moved the <12> block one place. In effect it has switched positions with the empty space, so this counts as one switch. The empty space is now in a grey position which means that the number of switches to solve the puzzle must be odd. Of course, to get back to the solved position, we just need one switch to get it back, and as one is an odd number, this puzzle can be solved.
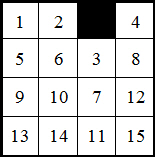 Starting from the solved position, the <15> block has switched across, then the <11>, <7> and the <3> came down. Although the <11> <7> and <3> could all have been moved together, it counts as three separate switches, so in total we’ve made four switches.
The empty space is in a black position indicating that we need an even number of switches to solve the puzzle. Four is an even number so the puzzle can be solved.
Starting from the solved position, the <15> block has switched across, then the <11>, <7> and the <3> came down. Although the <11> <7> and <3> could all have been moved together, it counts as three separate switches, so in total we’ve made four switches.
The empty space is in a black position indicating that we need an even number of switches to solve the puzzle. Four is an even number so the puzzle can be solved.
There’s a neat way to describe the position of the blocks in this arrangement: (15 0 3 7 11) The 0 represents the original empty space that was in the bottom right hand corner. To understand it, imagine there’s a little arrow after each number like this: (15 > 0 > 3 > 7 > 11). You then work along from the left and look at the numbers in pairs. The first two numbers (15 > 0) tell you that the 15 has taken the place of the 0. This is a single switch. Moving along, (0 > 3) tells you the space has taken the place of the 3, so that’s another switch. After that the (3 > 7) tells you the 3 has taken the 7 place, then (7 > 11) means the 7 is in the 11 place. So far we’ve had four switches. Finally the 11 has been forced into the only available position which is 15, but as it was forced, this does not count as a switch.
The effect is that these blocks and the space have all chased after each other round in a sequence. Bearing this in mind, writing (15 0 3 7 11) describes exactly the same pattern as (7 11 15 0 3) or ( 0 3 7 11 15). To see how many switches are involved, you count up the numbers in the bracket then subtract 1. This bracket has five numbers, so that indicates four switches.
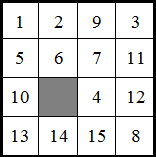 Suppose you're sitting on a bus and somebody has dropped a plastic tile puzzle scrambled up like this:
Suppose you're sitting on a bus and somebody has dropped a plastic tile puzzle scrambled up like this:
You’ll see the 4 is in the 11 position and the 11 is in the 8 position and so on. If you keep going you can work out the full sequence: ( 4 11 8 0 10 9 3) Obviously when the puzzle was scrambled up, it took several moves to get the 4 into the 11 position, but that doesn’t matter. (4>11) just counts as a single switch. The same applies to (11>8) and (8>0) and so on. Therefore as there are seven numbers in the bracket, the total number of switches is six, which is an even number.
 So can this puzzle be solved?
So can this puzzle be solved?
No! The empty square is in a grey position, which tells us it needs to be an odd number of switches. Whoever left the puzzle on the bus must have prised the tiles out and mixed them round to ruin somebody else’s day.
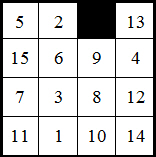 A shuffled puzzle can have more than one sequence of changed tiles. This messed up puzzle involves three sequences:
A shuffled puzzle can have more than one sequence of changed tiles. This messed up puzzle involves three sequences:
( 14 0 3 10 15 5 1) and (13 4 8 11) and (9 7)
To see if it can be solved you add up the switches for each bracket: 6 + 3 + 1 = 10
10 is an even number, and the empty space is on a black square, so this one can be solved!
Sam Loyd Sliding Puzzle Explanation |
|
|
|