|
|
We should like to apologise to any four wheel drive vehicle enthusiasts who have
found this page through a search engine and are just a TINY bit disappointed.

|
|
1= 44/44 2= 4/4 + 4/4 3= (4 + 4 + 4) / 4 4= 4 + (4 - 4) x 4 5= (4 x 4 + 4) / 4 6= (4 + 4) / 4 + 4 7= 4 + 4 - 4/4 8= 4 + 4 + 4 - 4 9= 4 + 4 + 4/4 10= (44 - 4) / 4 11= 44 / (SQRT4 + SQRT4) 12= 4 x 4 - SQRT4 x SQRT4 13= 44/4 +SQRT4 14= 4 x 4 - 4 + SQRT4 15= 4 x 4 - 4/4 16= 4+ 4 +4 + 4 17= 4 x 4 + 4/4 18= 4 x 4 + 4 - SQRT4 19= 4! - 4 - 4/4 20= (4 + 4) x SQRT4 + 4 21= (44 - SQRT4) / SQRT4 22= 4 x 4 + 4 + SQRT4 23= 4! + 4/4 - SQRT4 24= 4 x 4+ 4 + 4 25= (SQRT4 + SQRT4)! + 4/4 26= 4 x 4 + 4!! + SQRT4 27= 4! + SQRT4 + 4/4 28= 4! + 4 + 4 - 4 29= 4! + 4 + 4/4 30= 4! + 4 + 4 - SQRT4 31= 4! + 4!! - 4/4 32= 4! + 4!! + 4 - 4 33= 4! + 4!! + 4/4 34= 4! + 4!! + 4 - SQRT4 35= 4! + 4!! + (4!/4!!) 36= 4! + 4 + 4 + 4 37= 4! + (4! + SQRT4) / SQRT4 38= 4! + 4!! + 4 + SQRT4 39= 4! + (4 + 4/4)!! 40= 44 - SQRT4 - SQRT4 |
41= 44 - (4!/4!!) 42= 44 - 4 + SQRT4 43= 44 - 4/4 44= 44 + 4 - 4 45= 44 + 4/4 46= 44 + 4 - SQRT4 47= 44 + (4!/4!!) 48= 44 + SQRT4 + SQRT4 49= (4! x SQRT4) + 4/4 50= 44 + 4 + SQRT4 51= 4! x SQRT4 + (4!/4!!) 52= 44 + 4 + 4 53= ((4!!)!! + 4!)/ 4!! + SQRT4 54= 4! x SQRT4 + SQRT4 + 4 55= ((4!!)!! + 4!)/ 4!! + 4 56= 4! x SQRT4 + 4 + 4 57= (4!/4!!)^4 - 4! 58= 4!! x 4!! - 4 - SQRT4 59= ((4!!)!! + 4!)/ 4!! + 4!! 60= 4!! x 4!! - SQRT4 - SQRT4 61= 4!! x 4!! - (4!/4!!) 62= 4!! x 4!! - 4 + SQRT4 63= 4!! x 4!! - 4/4 64= 4!! x 4!! + 4 - 4 65= 4!! x 4!! + 4/4 66= 4!! x 4!! + 4 - SQRT4 67= 4!! x 4!! + (4!/4!!) 68= 4!! x 4!! + SQRT4 + SQRT4 69= ((4!)^SQRT4 - 4!)/ 4!! 70= 4!! x 4!! + 4 + SQRT4 |
71= ((4!)^SQRT4 - 4!!)/ 4!! 72= 4!! x 4!! + 4 + 4 73= ((4!/4!!)^4 - 4!! 74= 4!! x 4!! + 4!! + SQRT4 75= ((4!)^SQRT4 + 4!)/ 4!! 76= 4! x (4!/4!!) + 4 77= (4!/4!!)^4 - 4 78= 4!! x (4!! + SQRT4) - SQRT4 79= (4!/4!!)^4 - SQRT4 80= 4!! x (4 + 4 + SQRT4) 81= (4 - 4/4)^4 82= 4!! x (4!! + SQRT4) + SQRT4 83= (4!/4!!)^4 + SQRT4 84= 4!! x (4!! + SQRT4) + 4 85= (4!/4!!)^4 + 4 86= (4 + SQRT4)! / 4!! - 4 87= ((4 + SQRT4)! - 4!) / 4!! 88= (4 + SQRT4)! / 4!! - SQRT4 89= (4!/4!!)^4 + 4!! 90= (SQRT4 + SQRT4 + SQRT4)! / 4!! 91= ((4 + SQRT4)! + 4!!) / 4!! 92= 4! x 4 - SQRT4 - SQRT4 93= 4! x 4 - (4!/4!!) 94= 4! x 4 - 4 + SQRT4 95= 4! x 4 - 4/4 96= 4! x 4 + 4 - 4 97= 4! x 4 + 4/4 98= 4! x 4 + 4 - SQRT4 99= 4! x 4 + (4!/4!!) 100= (4 + 4 + SQRT4)^SQRT4 or 4! x 4 + SQRT4 + SQRT4 © Murderous Maths 2004 |
And here are all the solutions for numbers 101-200 and beyond!
|
101 = (4 + (4!/4!!))!! - 4 102 = ((4!!)!! + 4!)/ (SQRT4 + SQRT4) 103 = (4 + (4!/4!!))!! - SQRT4 104 = ((4!!)!! + 4!)/ 4 + SQRT4 105 = (4 + 4 - 4/4)!! 106 = ((4!!)!! + 4!)/ 4 + 4 107 = (4 + (4!/4!!))!! + SQRT4 108 = (4!! + SQRT4)^SQRT4 + 4!! 109 = (4 + (4!/4!!))!! + 4 110 = ((4!!)!! + 4!)/ 4 + 4!! 111 = 444/4 112 = (4 + 4/4)! - 4!! 113 = (4 + (4!/4!!))!! + 4!! 114 = (4 + SQRT4)! / 4!! + 4! 115 = ((4!!)!! + (4!!)!!! - 4)/4 116 = (4 + 4/4)! - 4 117 = ((4!!)!! + (4!!)!!! + 4)/4 118 = (4 + 4/4)! - SQRT4 119 = 4 x 4! + INT (SQRT(4!!)!!) + 4 120 = ((4 x 4 + 4)/ 4)! 121 = (44/4)^SQRT4 122 = (4 + 4/4)! + SQRT4 123 = 4 x 4! + INT (SQRT(4!!)!!) + 4!! 124 = 4x4! + 4! +4 125 = (((4!!)!! - 4!)/4!!) + (4!!)!!! 126 = (4^4/SQRT4) -SQRT4 127 = (((4!!)!! x 4!!) - 4!)/4! 128 = 4x4x4xSQRT4 129 = (((4!!)!! x 4!!) + 4!)/4! 130 = (4^4/SQRT4) + SQRT4 131 = (((4!!)!! + 4!)/4!!) + (4!!)!!! 132 = (4^4/SQRT4) + 4 133 = (4!! - 4/4) x INT(SQRT (4!!)!!) 134 = ((4!!)!!! x SQRT4) - 4! - SQRT4 135 = (4!! x INT(SQRT (4!!)!!)) -INT(SQRT (4!!)!!) + SQRT4 136 = (4^4/SQRT4) + 4!! 137 = (4!! x INT(SQRT (4!!)!!)) -INT(SQRT (4!!)!!) + 4 138 = (((4!)^SQRT4) - 4!)/4 139 = ((4!! + SQRT4)!!! - SQRT4)/SQRT4 140 = ((4!)^SQRT4)/4 - 4 |
141 = ((4!! + SQRT4)!!! + SQRT4)/SQRT4 142 = ((4!)^SQRT4)/4 - SQRT4 143 = (((4!)^SQRT4) - 4)/4 144 = (SQRT4 + SQRT4 + SQRT4) x 4! 145 = (((4!)^SQRT4) + 4)/4 146 = ((4!)^SQRT4)/4 + SQRT4 147 = (4!! x INT(SQRT(4!!)!!)) - 4 - INT(SQRT(SQRT4)) 148 = ((4!)^SQRT4)/4 + 4 149 = (4!! x INT(SQRT(4!!)!!)) - (4!/4!!) 150 = (((4!)^SQRT4) + 4!)/4 151 = ((4!!)!! - (4!!)!!! - SQRT4)/SQRT4 152 = ((4!)^SQRT4)/4 + 4!! 153 = ((4!!)!! - (4!!)!!! + SQRT4)/SQRT4 154 = ((4!!)!!! x SQRT4) - 4 - SQRT4 155 = INT(SQRT((4!!)!)) - INT(SQRT((4!!)!!)) -4! -SQRT4 156 = (4! + SQRT4) x (4!/4) 157 = ((4!!)!!! x SQRT4) - (4!/4!!) 158 = ((4! - 4) x 4!!) - SQRT4 159 = ((4!!)!!! x SQRT4) - 4/4 160 = (44-4) x 4 161 = ((4!!)!!! x SQRT4) + 4/4 162 = ((4! - 4) x 4!!) + SQRT4 163 = ((4!!)!!! x SQRT4) + (4!/4!!) 164 = (4! x 4!!) - 4! - 4 165 = INT(SQRT((4!!)!)) - INT(SQRT((4!!)!!)) -4! + 4!! 166 = (4! x 4!!) - 4! - SQRT4 167 = (4!!)!! - INT(SQRT((4!!)!)) - INT(SQRT((4!!)!!)) + SQRT4 168 = (4 + 4!/4!!) x 4! 169 = ((4! + SQRT4)/SQRT4)^SQRT4 170 = (4! x 4!!) - 4! + SQRT4 171 = INT(SQRT((4!!)!)) - INT(SQRT((4!!)!!)) -4!! - SQRT4 172 = (44 x 4) - 4 173 = INT(SQRT((4!!)!)) - 4! -(4!/4!!) 174 = (44 x 4) - SQRT4 175 = INT(SQRT((4!!)!)) - 4! -4/4 176 = 44 x SQRT4 x SQRT4 177 = INT(SQRT((4!!)!)) - 4! +4/4 178 = (44 x 4) + SQRT4 179 = ((4!!)!! - 4! - SQRT4)/SQRT4 180 = (4! x 4!!) - 4!! - 4 |
181 = ((4!!)!! - 4! + SQRT4)/SQRT4 182 = (4! x 4!!) - 4!! - SQRT4 183 = INT(SQRT((4!!)!)) - INT(SQRT((4!!)!!)) + SQRT4 184 = (4! x 4!!) - 4 - 4 185 = (4 + (4!/4!!))!! + (4!!)!!! 186 = (4! x 4!!) - 4 - SQRT4 187 = ((4!!)!! - 4!! - SQRT4)/SQRT4 188 = (4! x 4!!) - (SQRT4 x SQRT4) 189 = (4! x 4!!) - (4!/4!!) 190 = (4! x 4!!) - (4/SQRT4) 191 = (4! x 4!!) - (4/4) 192 = (4! x 4!!) x 4/4 193 = (4! x 4!!) + (4/4) 194 = (4! x 4!!) + (4/SQRT4) 195 = (4! x 4!!) + (4!/4!!) 196 = (4!! + 4 + SQRT4)^SQRT4 197 = ((4!!)!! +4!! +SQRT4)/SQRT4 198 = (4! x 4!!) + 4 + SQRT4 199 = INT(SQRT((4!!)!)) - (SQRT4 x SQRT4)/4 200 = (4! x 4!!) + 4 + 4 And here are just a few more... 201 = INT(SQRT((4!!)!)) + (SQRT4 x SQRT4)/4 202 = ((4!!)!! + 4! - 4)/SQRT4 203 = ((4!!)!! + 4! - SQRT4)/SQRT4 204 = ((4!!)!! + (SQRT4 x SQRT4)!)/SQRT4 205 = ((4!!)!! + 4! + SQRT4)/SQRT4 206 = ((4!!)!! + 4! + 4)/SQRT4 207 = INT(SQRT((4!!)!)) + 4 + 4!/4!! 208 = (4! x 4!!) + (4 x 4) 209 = INT(SQRT((4!!)!)) + 4!! +4/4 210 = (4 + 4!/4!!)!! x SQRT4) 211 = INT(SQRT((4!!)!)) + 4!! + 4!/4!! 212 = INT(SQRT((4!!)!)) + 4+ 4 +4 © Murderous Maths 2004 |
Many thanks to Sunny (Ana Marin) and Michael Jones who first
supplied these answers to us way back in 2004.
supplied these answers to us way back in 2004.
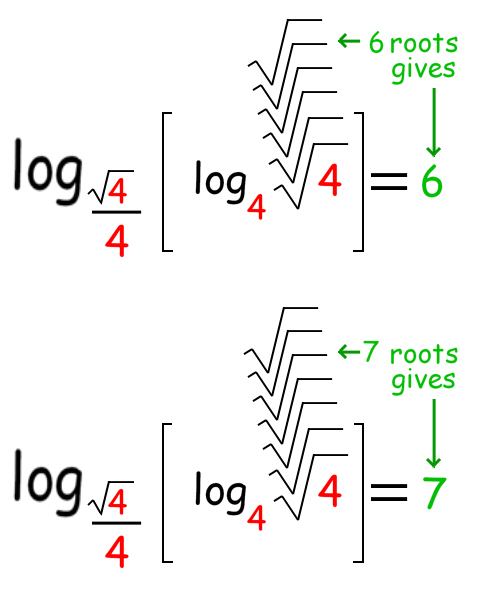
There is also an answer using the LOG function to create ANY number!All you have to do is increase the number of square root signs in the bracket. Pray tell, what is this sorcery? All is explained here by the brilliant Alex Bellos...
|
|


 HINTS
HINTS