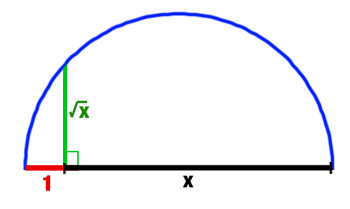
Square Roots without a calculator!

Lots of people have asked us how to get square roots without a calculator, and lots of others have sent us different ways of doing it!

You'll find the classic method written out for you in Easy Question Evil Answers.

There are other ways of working out square roots on this page. The first methods shown here are probably best for whole numbers, but then there's the proper method for decimals.

Method 1 (with no dividing but it's slower)

Suppose you want the square root of 75.
As 8² = 64 and 9² = 81, you know the answer is somewhere between the two.
Try working out 8.5² and you get 72.25 (too small)
Now try 8.6² and you get 73.96 (too small but getting closer)
Now try 8.7² and you get 75.69 (too big)
Now you know the answer is between 8.6 and 8.7
Now try working out 8.65² and you get 74.8225 (too small)
Now try 8.66² ... and so on.
Keep going until you get an answer that's accurate enough for you.

If you want
the square root of a perfect square
Mrs Brooksbank (a maths teacher) told us to subtract the odd numbers in order 1,3,5,7 etc. until you get to zero then count up the number of subtractions!
E.g. to get the square root of 36 it's:
36-1=35
35-3=32
32-5=27
27-7=20
20-9=11
11-11=0
Total number of subtractions = 6 therefore the square root of 36 = 6.

Method 2 (with nasty dividing but it's faster)

Again we'll try for the square root of 75.
As 8² = 64 and 9² = 81, you know the answer is somewhere between the two.
Guess it's 8.5 then work out 75/8.5 = 8.8235
Work out the average of 8.5 and 8.8235. It's (8.5 + 8.8235)/2 = 8.66175. This is a very close answer!
To get much closer, work out 75/8.66175 = 8.6588.
Work out the average of 8.66175 and 8.6588 to get 8.660275.
Hey - that's well close enough. 8.660275²=75.00036308. Now STOP SHOWING OFF.

Method 3 (using a formula)

KEITH FROM CANADA sent us this quick method which is usually accurate to about two decimal places. Here's his square root formula:
√X = √S + (X-S)/2√S
X = the number you want the square root of S = the closest square number you know to X

Let's try it on the square root of 75 again.
X=75 and so the nearest square number S = 81. This means that √S = 9.
Put the bits in the formula:
√75 = 9 + (75-81)/2*9
√75 = 9 + -6/18 = 9 - 0.333 = 8.667
Thanks Keith - we love it!

Short Cuts!
With some numbers you can make life easier for yourself and 75 is one of them.

Look and see if your number will divide by a square number. Here you'll see that 75 will divide by 25 and of course 25= 5². So you can put 75 = 25 x 3
If you work out the square roots you get sqrt(75) = sqrt(25) x sqrt(3).
sqrt (25)=5 and therefore sqrt(75)= 5 x sqrt3.
Of course you still need to know what sqrt(3) is, but the whole thing looks simpler now!
Thanks to "Shiney" for pointing this out to us!

We're very grateful to Frank La Fontaine from Australia who got in touch and explained the method he'd learnt at school 60 years ago! Of course the great thing about maths is that Frank's method will still work perfectly today. Here is his explanation in his own words - we've presented it here exactly as he sent it to us because we can't see how we'd make it any better!

Square Roots without a calculator!

Method 1 (with no dividing but it's slower)

Method 2 (with nasty dividing but it's faster)

Method 3 (using a formula)

Short Cuts!

Many thanks to Frank and everybody else who has helped us with this!

Murderous Maths Main Index Page

Method 1 (with no dividing but it's slower) Suppose you want the square root of 75. As 8² = 64 and 9² = 81, you know the answer is somewhere between the two. Try working out 8.5² and you get 72.25 (too small) Now try 8.6² and you get 73.96 (too small but getting closer) Now try 8.7² and you get 75.69 (too big) Now you know the answer is between 8.6 and 8.7 Now try working out 8.65² and you get 74.8225 (too small) Now try 8.66² ... and so on. Keep going until you get an answer that's accurate enough for you.	If you want the square root of a perfect square Mrs Brooksbank (a maths teacher) told us to subtract the odd numbers in order 1,3,5,7 etc. until you get to zero then count up the number of subtractions! E.g. to get the square root of 36 it's: 36-1=35 35-3=32 32-5=27 27-7=20 20-9=11 11-11=0 Total number of subtractions = 6 therefore the square root of 36 = 6.
Method 2 (with nasty dividing but it's faster) Again we'll try for the square root of 75. As 8² = 64 and 9² = 81, you know the answer is somewhere between the two. Guess it's 8.5 then work out 75/8.5 = 8.8235 Work out the average of 8.5 and 8.8235. It's (8.5 + 8.8235)/2 = 8.66175. This is a very close answer! To get much closer, work out 75/8.66175 = 8.6588. Work out the average of 8.66175 and 8.6588 to get 8.660275. Hey - that's well close enough. 8.660275²=75.00036308. Now STOP SHOWING OFF.
Method 3 (using a formula) KEITH FROM CANADA sent us this quick method which is usually accurate to about two decimal places. Here's his square root formula: √X = √S + (X-S)/2√S X = the number you want the square root of S = the closest square number you know to X Let's try it on the square root of 75 again. X=75 and so the nearest square number S = 81. This means that √S = 9. Put the bits in the formula: √75 = 9 + (75-81)/2*9 √75 = 9 + -6/18 = 9 - 0.333 = 8.667 Thanks Keith - we love it!
Short Cuts! With some numbers you can make life easier for yourself and 75 is one of them. Look and see if your number will divide by a square number. Here you'll see that 75 will divide by 25 and of course 25= 5². So you can put 75 = 25 x 3 If you work out the square roots you get sqrt(75) = sqrt(25) x sqrt(3). sqrt (25)=5 and therefore sqrt(75)= 5 x sqrt3. Of course you still need to know what sqrt(3) is, but the whole thing looks simpler now! Thanks to "Shiney" for pointing this out to us!