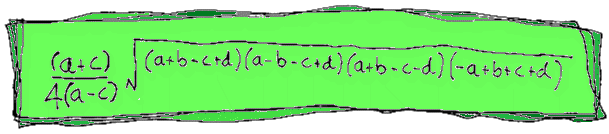We've found a real utterly nutty
PURE MATHEMATICIAN!
Regular visitors to the site will know this character...

but we had no idea she really exists AND she has even found a useful role to play in the community by being a maths teacher!

Big respect and thanks to the wonderful Pam Garnett of Wolfreton School for letting us use her photo!
|
THE RESEARCH LAB
Welcome! This is where our Pure Mathematicians experiment on little
bits of maths and try to answer some big questions.
If there's a question that YOU would like us to investigate, then
please contact us through the mailroom. If we
think it's interesting* enough and we can come up with an answer then you might see
it here... eventually!
* HINT: Don't ask us if 1 is a prime number. Been there,
done that, got nowhere, gave up, came home and put the kettle on.
* Also please DON'T
ask us to do long sums that you could do yourself on a calculator!
Sorry!
We're not allowed to do your maths homework for you. Obviously we'd like to,
but we get into trouble. So don't ask.
Thanks.
|
GUARANTEE: You may rest assured that no numbers or sums are harmed during
the course of our investigations.
Here are the answers to some of the questions that we've already been asked.
WHAT IS THE AREA OF AN ANULUS (or RING)?
asked (and answered) by Alex Jeffreys
 First of all we better see what an anulus is. It's the posh name for the red bit of this picture - so it's like a
disc with a hole in it, or a washer or a ring or a squashed doughnut.
First of all we better see what an anulus is. It's the posh name for the red bit of this picture - so it's like a
disc with a hole in it, or a washer or a ring or a squashed doughnut.
Obviously you can work out the area by subtracting the area of the little circle from the area of
the big circle, and to work out these areas you need to know the
radii of both circles.
HOWEVER... it's possible to get the area of the red bit with just one measurement!
We thought you might like to think about how to do this before you look at...
the area of an anulus answer!
WHAT IS THE SQUARE ROOT OF i?
asked by Phil M. of Manchester
In
Numbers - the Key to the Universe we meet the very spooky imaginary
number "i", which is the square root of -1. Therefore you can write:
i2 = -1
Understanding all about i is tough enough, but just to be awkward Phil
asked us, what is the square root of i?

|
It took a while but we think we've got it:
|
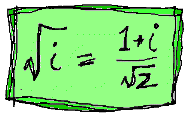
|
And what's more... we can prove it! If you square it, you get i. Look:
|
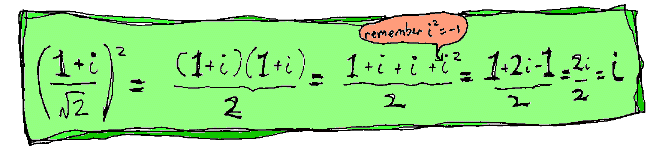
|
If you don't quite understand how we make the (1+i)2 bracket turn
into (1+i)(1+i) and then 1 +i +i+ i2, it's all explained in The Phantom X
What is the cube root of i?
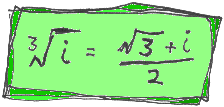 We had the square root of i on our site for ages, but LOTS of people demanded to know what is the cube root of i. Luckily that's not too ugly as you'll see here.
We had the square root of i on our site for ages, but LOTS of people demanded to know what is the cube root of i. Luckily that's not too ugly as you'll see here.
There are actually two more cube roots of i, and one of them is just -i!
If you work out (-i)3 you get (-i)×(-i)×(-i) = -(i×i×i) = -(-1×i) = i.
Thanks to GOSHKO for telling us this!
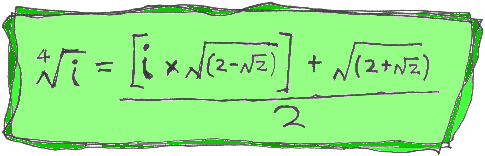 Then it got silly. People then demanded to know what is the FOURTH root of i. Here it is and it serves you right...
Then it got silly. People then demanded to know what is the FOURTH root of i. Here it is and it serves you right...
 And yes, we were even asked for the fifth root of i. There are a few answers to this (including 0.951056516 + 0.309016994i) but because i5 = i there is one very simple answer: i.
And yes, we were even asked for the fifth root of i. There are a few answers to this (including 0.951056516 + 0.309016994i) but because i5 = i there is one very simple answer: i.
While we're dealing with "i" here are some more questions we were asked:
What is the square root of -i ?
asked by Kitty Soft
You just multiply the answer for the square root of i (see above) by i.
You get SQRT(-i) = (i-1)/SQRT2
If i2=-1 then what does -i2=?
asked by Alex Jeffreys
You've got to be careful here. Usually -i2 would mean (-i)2 and we think that
ALSO makes -1.
However if you're not squaring the "-" then you're working out -(i)2 and that makes +1.
What does ii=?
asked by loads of people
This is very strange. The answer is a real number: 0.207879576...
What makes it even stranger is that there are a lot more answers. This all comes from Euler's Formula, so guess what the next question is?
WHAT IS EULER'S FORMULA?
Here it is:
eiθ =
cosθ + i sinθ
To understand this you need to know about e and angles measured in radians, which means that an angle of π = 180º .
The special case where θ = π gives us
eiπ =
cosπ + i sinπ but cosπ = -1 and sinπ = 0 so we end up with the utterly lovely equation ...
 Euler's Identity: eiπ = -1
Euler's Identity: eiπ = -1
 WHAT IS THE AREA OF AN ELLIPSE?
first asked by Jake Chan
WHAT IS THE AREA OF AN ELLIPSE?
first asked by Jake Chan
In
Vicious Circles and other Savage Shapes there's a chapter about
ellipses and loads of people asked how to work out their area. This diagram shows
the simple answer, but it's such a good question that we explained it in more detail
on a separate page which also tells you about "ellipsoids". (Incidentally, the ellipse
page is one of the most visited pages on the whole site!)
Have a look at: The Area of an Ellipse.
WHAT IS AN ARCTAN?
asked by Jordan Watts
In "Do You Feel Lucky"
it says that you can calculate PI using the fomrula
PI = 4[ARCTAN(1/2)+ARCTAN(1/3)]. Easy!
(You have to work this out in radians by the way, not degrees.)
ARCTAN is the inverse of TAN, which comes up in trigonometry and is a way of turning
fractions into angles. If you put TAN 45o into a calculator you should get the
answer 1. Or, you can put this the other way round, if you put the inverse of TAN 1
(or SHIFT TAN 1) into a calculator you get 45o. You can also say the ARCTAN
of 1 is 45o.
You can also have ARCSIN and ARCCOS. E.g.
SIN 30o=0.5 so ARCSIN 0.5=30o
 HOW CAN I FIND THE CENTRE OF A CIRCLE?
HOW CAN I FIND THE CENTRE OF A CIRCLE?
asked by Mello
There are several ways, but our favourite is the USING A BOOK method!
HOW DO YOU WORK OUT SQUARE ROOTS ONLY USING A PENCIL
AND PAPER?
asked by Alistair Lynn
We've had several answers to this, and now you'll find them on a separate page:
How to work out Square Roots without a calculator
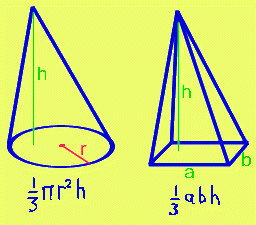 WHAT IS THE VOLUME OF A CONE (or a pyramid)?
asked by Aryan S. and others
WHAT IS THE VOLUME OF A CONE (or a pyramid)?
asked by Aryan S. and others
The volume of a cone, or any other pyramid shaped object is:
1/3 x base area x perpendicular height
These
two doodles show the volumes of a cone and a rectangular based pyramid.
Notice that the point of the pyramid (called "the apex") doesn't have to be directly above the middle of the base.
It can be leaning over a bit if you want, just so long as you measure the perpendicular height correctly.

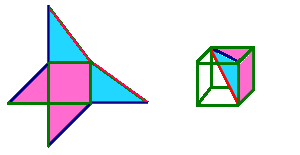
|
|
If the green sides all measure "1" then the blue sides measure sqroot2 and the red
sides measure sqroot3.
|
You can show this formula works for one sort of pyramid by using this net. If you cut it
out and fold it, you'll get a pyramid which has a square base and the apex
is directly above one of the corners. If
you make THREE of these pyramids you can put them together to make a perfect cube. The outside faces of the
cube will be pink, and the blue faces will not be seen.
The little diagram shows how the internal faces meet.
Obviously the cube volume = the height x the base area.
Also the cube volume = 3x each pyramid volume.
Therefore the volume of each pyramid = 1/3 x the height x the base area.
HOW CAN I WORK OUT THE nth TERM OF THE
FIBONACCI SERIES?
asked by Seung Yun Jee
Fibonacci's Series
This is a row of numbers, and each number in the row
equals the last two numbers added together. If the first two numbers
in the series are 1 and 1, then the next number is 1+1=2. The next number is
1+2=3 then 2+3=5 and so on. The series starts
1 1 2 3 5 8 13 21 34 55 89 144 ...
How to get the series from Pascal's Triangle!
|
In
NUMBERS - The Key To The Universe we meet the Fibonacci
series and how it creates the special number
known as the "golden ratio" or "divine proportion". This number has a special sign which is the Greek
letter called Phi.
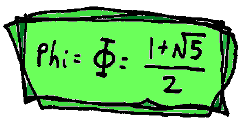
To get each number in the Fibonacci series you have to add the last two numbers together - but
suppose you want to know the 47th number, do you have to work out ALL the first 46
numbers? The answer is NO - thanks to a formula which uses the magic of Phi.
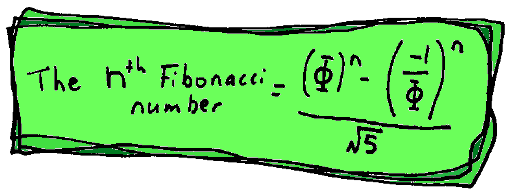
If you want the 47th Fibonacci number, you just put 47 in place of n and work it out.
In case you think this is too ugly, here we've replaced the Phi sign with its value:
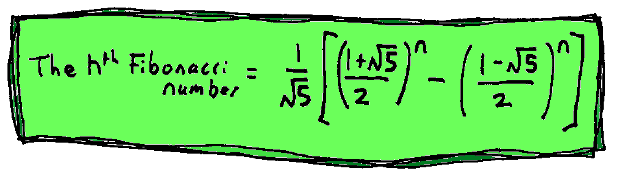
There are two things to know about this formula...
- You need a really good calculator to work out the powers!
- Even though it's full of square roots of five - amazingly the formula ALWAYS gives
a whole number as the answer!
There's more about this strange series on our
Fibonacci and Nature page
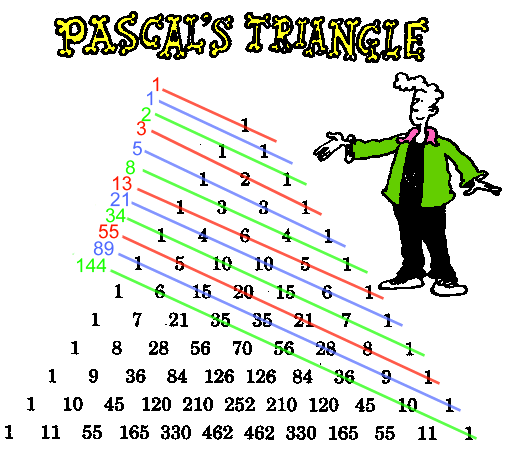 HOW DO I GET THE FIBONACCI SERIES FROM PASCAL'S TRIANGLE?
asked by Rex
HOW DO I GET THE FIBONACCI SERIES FROM PASCAL'S TRIANGLE?
asked by Rex
In Do You Feel Lucky? we find out why
Pascal's Triangle is one of the neatest things in maths. It's so groovy and it does so much weird
stuff that we didn't have room to put it all in. One of the strangest things it can do is
create the Fibonacci Series. (See the above question
to find out what the Fib series is.)
- You need to draw a Pascal's triangle starting with a 1 by itself at the top. (You can find out
how to do this on our Pascal's Triangle Page )
- You then draw in a set of diagonal lines like in our diagram.
- If you add up the numbers on the lines
you get the Fibonacci series!
It's not too surprising that Pascal's Triangle produces the Fibonacci series in some strange way.
After all, each number on the triangle equals the two numbers above it added together and each number
in the series are the two numbers before it added together.
WHAT ARE THE FIRST 100 ROWS OF PASCAL'S TRIANGLE?
asked by Alice
Not enough space here sadly (and exactly WHY do you want to know anyway?)
but if you really want to see a Pascal Triangle that sings and dances,
go to Dolly's Links
and try the The Self-Colouring Pascal's Triangle. It's brilliant!
HOW MANY DIFFERENT NETS ARE THERE THAT MAKE A CUBE?
asked by Bob
In Vicious Circles we find out about "nets" which are
flat shapes that fold into solid objects. If you put six squares together
you can make a net that folds into a cube. Our challenge was to find out how
many ways you can arrange your six squares to start with! If you don't count rotations
or reflections, we think there are 11 different nets in total, and you can
see them all here in this lovely picture.
Of course you can make other patterns
with six squares, but they won't fold together to make a cube!
 While we're talking about nets, LOADS of people keep asking us:
While we're talking about nets, LOADS of people keep asking us:
WHAT IS THE NET OF A SPHERE?
About the closest you can get to it is peel an orange VERY CAREFULLY so that all
the skin comes off in one bit then squash it flat.
Pssst... we have to admit, that answer makes us feel rather pleased with ourselves!
  THE NUMBER ZONE
THE NUMBER ZONE
We get lots of questions about odd sums and things. Here are some of our favourites.
MIKE asked: 138 x 42 = 5796 Is there another multiplication like this that uses
all the digits 1-9?
Big respect to JAMIE WALLHEAD who came up with:
157 x 28 = 4396 159 x 48 = 7632 186 x 39 = 7254
198 x 27 = 5346 297 x 18 = 5346 483 x 12 = 5796
TIM asked: Is there a fraction that turned into a decimal uses all the digits 0-9
repeating?
Yes indeed. 137174210/1111111111 = 0.12345678901234567890...
Some other interesting results are: 1/81 = 0.012345679 012345679 01234... (shame about the 8's)
Also 1/9801 = 0.00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23....
Jonathan Mui asked: WHAT IS THE LOWEST NUMBER TO BE A PERFECT SQUARE AND A PERFECT CUBE?
It's 1 because 12=1 and 13=1. Easy! In case you're interested,
the next one is 64 which is 82 and 43 and also 26.
WILL asked: WHAT IS THE LOWEST NUMBER THAT DIVIDES EXACTLY BY EVERY NUMBER BETWEEN 1-20?
Will thought it was 338268752640 but actually it's
232,792,560 ... which also divides by 21 and 22.
So just to be difficult
SONNY asked us: WHAT IS THE LOWEST NUMBER THAT DIVIDES EXACTLY BY EVERY NUMBER BETWEEN 1-100?
Get ready! Its:
69,720,375,229,712,477,164,533,808,935,312,303,556,800
|
 JORDAN WATTS saw on our Perfectly Useless Facts Page that...
JORDAN WATTS saw on our Perfectly Useless Facts Page that...
153, 370, 371 and 407 are all equal to the sums of the cubes of their digits.
(e.g. 153 = 13 + 53 +33 = 1 + 125 + 27)
So Jordan asked if there any numbers that are equal to the sums of the 4th powers of the digits?
Harry W told us we should be looking out for NARCISSISTIC NUMBERS. Suppose you have a number with N digits. If you put each digit to the Nth power and then add them up, you get the orginal number. There are 88 narcissistic numbers in total. 153, 370, 371 and 407 are the three-digit narcissisitic numbers.
Many thanks to Steven Charlton, Thomas
Gooderidge and Michael Jones who supplied these narcissistic numbers:
1,634 = 14 + 64 + 34 + 44 = 1 + 1296 + 81 + 256
8,208 = 84 + 24 + 04 + 84 = 4096 + 16 + 0 + 4096
9,474 = 94 + 44 + 74 + 44 = 6561 + 256 + 2401 + 256
54,748 = 55 + 45 +75 +45 + 85
= 3125 + 1024 + 16807 + 1024 + 32768
92,727 = 95 + 25 + 75 + 25 + 75
93,084 = 95 + 35 + 05 + 85 + 45
548,834 = 56 + 46 + 86 + 86 + 36 + 46
And then Michael got a bit carried away...
1,741,725 = 17 + 77 + 47 + 17 + 77 + 27 + 57
4,210,818 = 47 + 27 + 17 + 07 + 87 + 17 + 87
9,800,817 = 97 + 87 + 07 + 07 + 87 + 17 + 77
9,926,315 = 97 + 97 + 27 + 67 + 37 + 17 + 57
24,678,050 = 28 + 48 + 68 + 78 + 88 + 08 + 58 + 08
And then Steven Charlton got even MORE carried away. He designed his own computer programme to work out that...
146511208, 472335975, 534494836, 912985153 are all equal to sums of the 9th powers of their digits.
4679307774 is equal to the sum of the 10th power of its digits.
... and then Michael sent us the BIGGEST narcissistic number:
115,132,219,018,763,992,565,095,597,973,971,522,401 has 39 digits AND it is the sum of the 39th
powers of its digits.
In other words it equals 139 +139 +539 +139 +339 + ... +439 +039 +139.
And THEN, to make things even more exciting, Michael sent us something slightly different...
3,435 is equal to the sums of the digits raised to the powers of themselves i.e.
3,435 = 33 +44 +33 +55.
...and... 40,585 is the sum of the
factorials of its digits so 4! + 0! + 5! + 8! + 5! = 40,585
About 5 years after we found out all the things you've just read, Kevin Wilson got in touch and told us that:
145 = 1! + 4! + 5!
And Xende told us that:
33 + 43 + 53 = 63
FINALLY Kevin Wilson (again!) told us a cute thing about the numbers 89, 135 and 1306:
81 + 92 = 89
11 + 32 + 53= 135
11 + 32 + 03 + 64= 1306
|
HOW CAN I FIND THE AREAS OF REGULAR POLYGONS?
asked by Steve Charlton
If your polygon has n sides and the side length is s then...
AREA OF POLYGON = ns2 / 4{tan(180/n)}
|
So if you have a regular hexagon that measures 4cm each side, you use s=4 and n=6. You get:
AREA = 6*4*4 / 4[tan(180/6)] = 24 / [tan(30)] = 24 / 0.577 = 41.569 sq cm.
WHAT IS THE VOLUME OF A TORUS?
asked by Shanthan Golden
In case you don't know, a TORUS is like a cylinder curled round and joined up
to make a circle, which ends up looking like a lifebelt or doughnut shape.
There are two
formulas for the volume depending on which measurements you've got.
R = the distance from the centre of the hole in the middle to the
centre of the cylinder, and r = the radius of the cylinder.
|
a =the distance from the centre of the hole in the middle to the inside edge and b =
the distance from the centre of the hole to the outside edge.
|
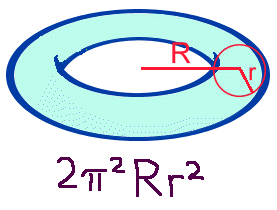 |
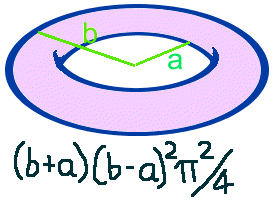 |
We love these formulas because you get PI squared. It doesn't happen very often!
Why does 0.99999... = 1 ?
asked by loads of people!
You'll find the answer HERE
A factorial multiplies the number by all the smaller numbers
down to 1. For example
4! = 4 x 3 x 2 x 1 = 24
3! = 3 x 2 x 1 = 6
2! = 2 x 1 =2
1! is just 1 (obviously)
|
WHY DOES 0! =1 ?
asked by "The Mathster"
In the book
Do You Feel Lucky? we use a lot of "factorials" in sums.
A factorial has a sign like this: !
But the BIG question is: what does 0! = ? The answer is also 1.
In the book we showed how our first investigations went:

However this wasn't good enough for a supervillain known as
"The Mathster". He challenged us to give a proper reason, and this
is the best we came up with:
- If you have 3 playing cards in your hand, you can arrange them in 3! different ways.
In other words you can put them in 3 x 2 x 1 = 6 different orders.
(It's all explained in "Do You Feel Lucky?")
- If you have 2 cards, you can put them in 2! different ways which is 2.
- If you just have 1 card you can only arrange it 1! ways which is 1.
- But if you have ZERO cards then there's also one way of doing that!
You might have to think about the last bit like this: if there was NO way
of having zero cards, then wherever you went or whatever you were doing,
it would be impossible not to have at least one card on you. Even if you were in the bath.
So 0! = 1.
That was our best answer, but several other Murderous Maths fans sent in their answers.
We especially liked this one:
GAIL WEISS says: 4! = 4x3x2x1 and 3!=3x2x1. Therefore 4!=4x3!
In the same way 3!=3x2! and 2!=2x1! So it follows that 1!=1x0!
Therefore 0! must =1 or 1! would be 0 and so 2! would be zero and then 3!
would be zero...and so on.
Let us hope that The Mathster now stops bothering us with
tough questions and blends back into his secret civilian identity which is being a Murderous Maths
fan called David Small.
 WHAT DOES 0/0 EQUAL?
asked by Alex Jeffries
WHAT DOES 0/0 EQUAL?
asked by Alex Jeffries
Alex went on to ponder: Does 0/0 = 1 because both numbers are the same,
or is it 0 because there's nothing involved?
We had fun checking this one, but our final results are something like this:
If you have a bag containing 0 chips and share them between no people, how
many do they each get?
However somebody called "KOO C W" came up with this for us:
Because anything x 0 = 0 therefore 0/0 can = anything.
Good one!
HOW CAN YOU FIND THE VOLUMES OF THE REGULAR SOLIDS?
asked by Joe Symons-Smyth
A regular solid is a lump that has all sides the same length, all faces the
same shape and the same number of sides meeting at every corner. There are only
five of them, you can see what they look like here:
Regular Solids.
If you want to read all about the regular solids, they are described properly
in the MM book Vicious Circles .
|
As Joe pointed out, you can easily get the volume of a cube by measuring one side
and cubing it. So if the side measures "s" the volume of a cube = s3.
The challenge was to find formulas for the other regular solids!
We've finally got the answers which are on their own special page:
Regular Solid Volumes.
WHAT IS THE HIGHEST PRIME NUMBER EVER CALCULATED?
asked by "MooCow"
PRIME NUMBERS
If you want to know what prime numbers are, it's all explained with
a special prime number calculator and a good trick on our
Prime Number Page
|
Good question! You can get the answer yourself on one of our favourite websites:
News of the BIGGEST prime number found so far!
WHAT IS THE DIFFERENCE BETWEEN A NORMAL
PRIME AND A MERSENNE PRIME NUMBER?
asked by Piyush "Fat Boy" Singh
In the NUMBERS book we meet Mersenne primes which
have to fit the formula (2n-1). By the way, not all numbers that fit the formula are primes,
just some of them.
So a NORMAL prime can be any prime number, but to be a Mersenne prime when you add 1 it must
make a power of 2.
- 17 is prime but it is NOT a Mersenne prime because 17+1 = 18 which isn't a power of 2.
- 31 IS a Mersenne prime because 31+1=32= 25
EXACTLY WHAT IS AN OBLONG?
We were told this by Katherine Barker
In the dictionary, "oblong" means that a shape is longer than it is wide, so
if you have a shape called an oblong it could be an ellipse, but more usually it's
a rectangle. It's the rectangle bit that's confusing so just to clear things up:

- An oblong can be a rectangle but it cannot be a square.
- A square is a rectangle, but it is not an oblong.
- A rectangle can be a square or an oblong.
HOW CAN I WORK OUT THE AREA OF A TRAPEZIUM IF I ONLY
KNOW THE LENGTHS OF THE FOUR SIDES?
asked by "Roberdin"
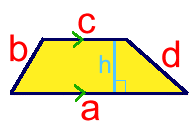 This is a REAL beauty! Normally to work
out the area of a trapezium you need to know
the height between the parallel sides. In this diagram the area would be:
This is a REAL beauty! Normally to work
out the area of a trapezium you need to know
the height between the parallel sides. In this diagram the area would be:
AREA = h(a+c)/2
But what if you don't know the height or any angles?
At first we thought it was impossible, but lots of people told us differently!
Here's the formula we finally worked out for the area of a trapezium where sides a and c
are parallel:
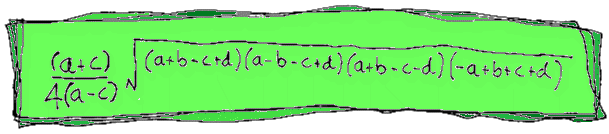
As you'll be desperate to know how we got this amazing result, take a look at our special
TRAPEZIUM AREA page!
And here's one that's too simple to bother with...
THOMAS JOHNSON asks us: Is it possible to reconstruct the Maclaurin/Taylor series
of successive derivatives to make it converge faster to evaluate "e" to a higher
degree of accuracy?
Don't patronise us, Thomas!
|

Go to the Mailroom and ask YOUR question!
Murderous Maths Main Index Page




 First of all we better see what an anulus is. It's the posh name for the red bit of this picture - so it's like a
disc with a hole in it, or a washer or a ring or a squashed doughnut.
First of all we better see what an anulus is. It's the posh name for the red bit of this picture - so it's like a
disc with a hole in it, or a washer or a ring or a squashed doughnut.

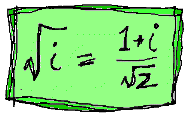
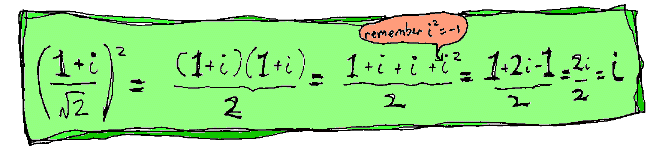
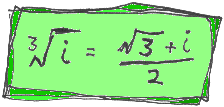 We had the square root of i on our site for ages, but LOTS of people demanded to know what is the cube root of i. Luckily that's not too ugly as you'll see here.
We had the square root of i on our site for ages, but LOTS of people demanded to know what is the cube root of i. Luckily that's not too ugly as you'll see here.
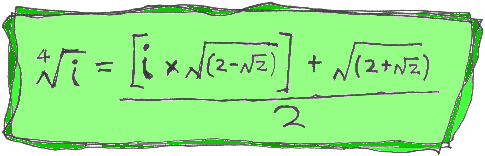 Then it got silly. People then demanded to know what is the FOURTH root of i. Here it is and it serves you right...
Then it got silly. People then demanded to know what is the FOURTH root of i. Here it is and it serves you right...
 And yes, we were even asked for the fifth root of i. There are a few answers to this (including 0.951056516 + 0.309016994i) but because i5 = i there is one very simple answer: i.
And yes, we were even asked for the fifth root of i. There are a few answers to this (including 0.951056516 + 0.309016994i) but because i5 = i there is one very simple answer: i.
 Euler's Identity: eiπ = -1
Euler's Identity: eiπ = -1
 WHAT IS THE AREA OF AN ELLIPSE?
first asked by Jake Chan
WHAT IS THE AREA OF AN ELLIPSE?
first asked by Jake Chan HOW CAN I FIND THE CENTRE OF A CIRCLE?
HOW CAN I FIND THE CENTRE OF A CIRCLE?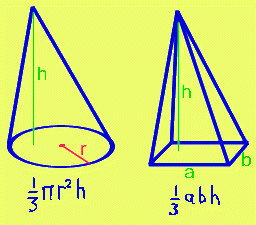 WHAT IS THE VOLUME OF A CONE (or a pyramid)?
asked by Aryan S. and others
WHAT IS THE VOLUME OF A CONE (or a pyramid)?
asked by Aryan S. and others
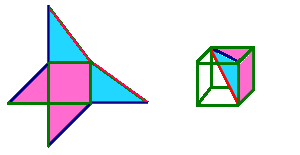
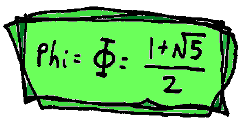
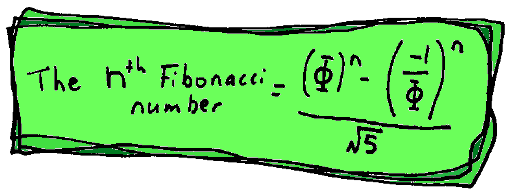
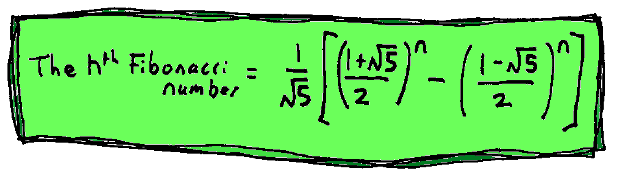
 HOW DO I GET THE FIBONACCI SERIES FROM PASCAL'S TRIANGLE?
asked by Rex
HOW DO I GET THE FIBONACCI SERIES FROM PASCAL'S TRIANGLE?
asked by Rex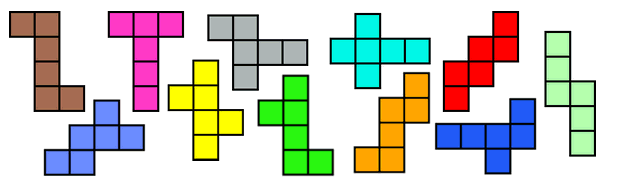
 While we're talking about nets, LOADS of people keep asking us:
While we're talking about nets, LOADS of people keep asking us:

 THE NUMBER ZONE
THE NUMBER ZONE


 WHAT DOES 0/0 EQUAL?
asked by Alex Jeffries
WHAT DOES 0/0 EQUAL?
asked by Alex Jeffries
 This is a REAL beauty! Normally to work
out the area of a trapezium you need to know
the height between the parallel sides. In this diagram the area would be:
This is a REAL beauty! Normally to work
out the area of a trapezium you need to know
the height between the parallel sides. In this diagram the area would be: